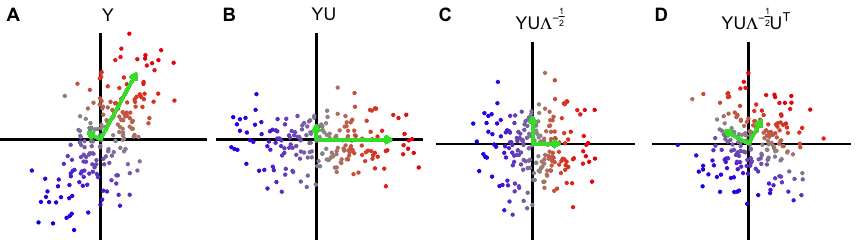
Data whitening is a widely used preprocessing step to remove correlation structure since statistical models often assume independence (Kessy, et al. 2018). The typical procedures transforms the observed data by an inverse square root of the sample correlation matrix (Figure 1). For low dimension data (i.e. \(n > p\)), this transformation produces transformed data with an identity sample covariance matrix. This procedure assumes either that the true covariance matrix is know, or is well estimated by the sample covariance matrix. Yet the use of the sample covariance matrix for this transformation can be problematic since 1) the complexity is \(\mathcal{O}(p^3)\) and 2) it is not applicable to the high dimensional (i.e. \(n \ll p\)) case since the sample covariance matrix is no longer full rank.

Here we use a probabilistic model of the observed data to apply a whitening transformation. Our Gaussian Inverse Wishart Empirical Bayes (GIW-EB) 1) model substantially reduces computational complexity, and 2) regularizes the eigen-values of the sample covariance matrix to improve out-of-sample performance.

devtools::install_github("GabrielHoffman/decorrelate")