bayesSSM is an R package offering a set of tools for performing
Bayesian inference in state-space models (SSMs). It implements the
Particle Marginal Metropolis-Hastings (PMMH) in the main function
pmmh for Bayesian inference in SSMs.
While there are several alternative packages available for performing Particle MCMC, bayesSSM is designed to be simple and easy to use. It was developed alongside my Master’s thesis about Particle MCMC, since I was implementing everything from scratch anyway.
In some state-space models, the full joint density of latent states and observations
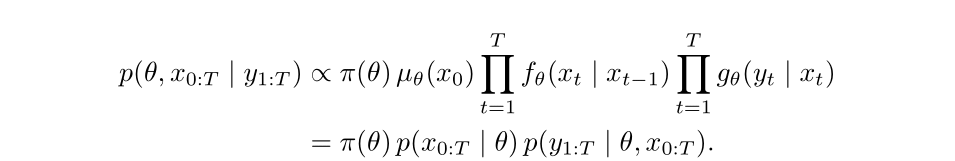
can be written out explicitly. In these cases, inference tools like Stan (which uses Hamiltonian Monte Carlo) are very efficient.
However, many real-world models define the latent dynamics only through a simulator, not via an explicit transition density. This includes:
In these cases, the joint posterior density cannot be computed directly, and the marginal likelihood is intractable. Thus, standard MCMC methods like Hamiltonian Monte Carlo (HMC) or Metropolis-Hastings (MH) cannot be applied directly.
The Particle Markov Chain Monte Carlo (PMCMC) methods, such as the Particle Marginal Metropolis-Hastings (PMMH) implemented in this package, are designed to handle these situations. They use particle filters to approximate the marginal likelihood and allow for efficient sampling from the posterior density of the latent states and parameters.
A state-space model (SSM) has the structure given in the following diagram, where we omitted potential time dependency in the transition and observation densities for simplicity.
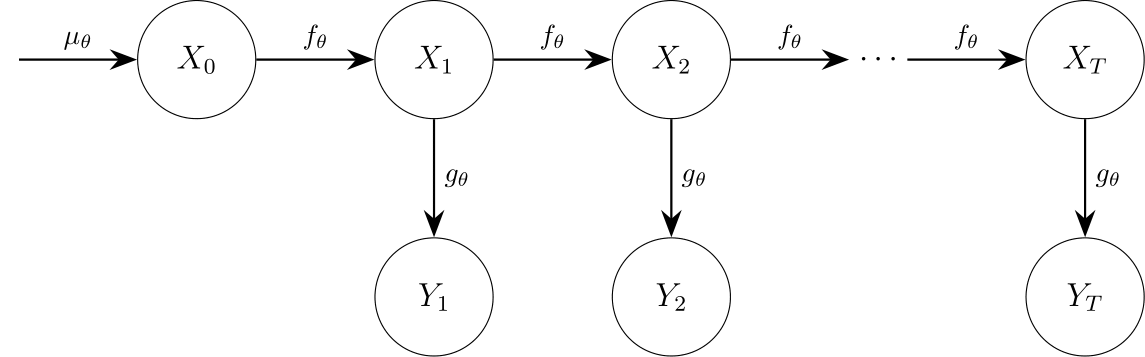
The core function, pmmh, implements Particle Marginal
Metropolis-Hastings, which is an algorithm that first generates a set of
\(N\) particles to approximate the
intractable marginal likelihood and then uses this approximation in the
acceptance probability. The implementation automatically tunes the
number of particles and the proposal distribution for the
parameters.
You can install the latest stable version of bayesSSM from CRAN with:
install.packages("bayesSSM")or the development version from GitHub with:
# install.packages("pak")
pak::pak("BjarkeHautop/bayesSSM")To illustrate how to use the pmmh function, we will
simulate a simple state-space model (SSM) and perform Bayesian inference
on it. Note: While this example uses pmmh, the model is
simple enough that standard MCMC methods could also be applied. For a
more complicated example where standard MCMC methods cannot be used, see
the article Stochastic SIR Model article here.
We will simulate a state-space model with the following structure:
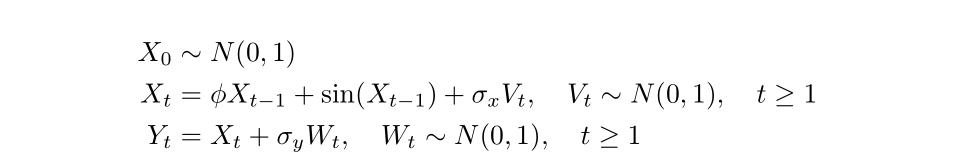
Let’s first simulate 20 data points from this model with \(\phi = 0.8\), \(\sigma_x = 1\), and \(\sigma_y = 0.5\).
set.seed(1405)
t_val <- 20
phi <- 0.8
sigma_x <- 1
sigma_y <- 0.5
init_state <- rnorm(1, mean = 0, sd = 1)
x <- numeric(t_val)
y <- numeric(t_val)
x[1] <- phi * init_state + sin(init_state) +
rnorm(1, mean = 0, sd = sigma_x)
y[1] <- x[1] + rnorm(1, mean = 0, sd = sigma_y)
for (t in 2:t_val) {
x[t] <- phi * x[t - 1] + sin(x[t - 1]) + rnorm(1, mean = 0, sd = sigma_x)
y[t] <- x[t] + rnorm(1, mean = 0, sd = sigma_y)
}
x <- c(init_state, x)We define the priors for our model as follows:
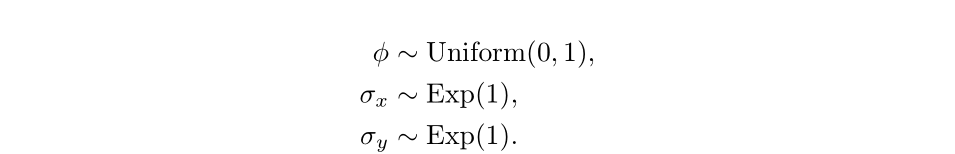
We can use pmmh to perform Bayesian inference on this
model. To use pmmh we need to define the functions for the
SSM and the priors.
The functions init_fn, transition_fn should
be functions that simulate the latent states. init_fn must
contain the argument num_particles for initializing the
particles, and transition_fn must contain the argument
particles, which is a vector of particles, and can contain
any other arguments for model-specific parameters.
The function log_likelihood_fn should be a function that
calculates the log-likelihood of the observed data given the latent
state variables. It must contain the arguments y for the
data and particles. Time dependency can be implemented by
giving a t argument in transition_fn and
log_likelihood_fn.
init_fn <- function(num_particles) {
rnorm(num_particles, mean = 0, sd = 1)
}
transition_fn <- function(particles, phi, sigma_x) {
phi * particles + sin(particles) +
rnorm(length(particles), mean = 0, sd = sigma_x)
}
log_likelihood_fn <- function(y, particles, sigma_y) {
dnorm(y, mean = particles, sd = sigma_y, log = TRUE)
}The priors for the parameters must be defined as log-prior functions.
Every parameter from init_fn, transition_fn,
and log_likelihood_fn must have a corresponding log-prior
function.
log_prior_phi <- function(phi) {
dunif(phi, min = 0, max = 1, log = TRUE)
}
log_prior_sigma_x <- function(sigma) {
dexp(sigma, rate = 1, log = TRUE)
}
log_prior_sigma_y <- function(sigma) {
dexp(sigma, rate = 1, log = TRUE)
}
log_priors <- list(
phi = log_prior_phi,
sigma_x = log_prior_sigma_x,
sigma_y = log_prior_sigma_y
)Now we can run the PMMH algorithm using the pmmh
function. For this README we use a lower number of samples and a smaller
burn-in period, and also modify the pilot chains to only use 200
samples. This is done to make the example run faster.
library(bayesSSM)
result <- pmmh(
y = y,
m = 500, # number of MCMC samples
init_fn = init_fn,
transition_fn = transition_fn,
log_likelihood_fn = log_likelihood_fn,
log_priors = log_priors,
pilot_init_params = list(
c(phi = 0.4, sigma_x = 0.4, sigma_y = 0.4),
c(phi = 0.8, sigma_x = 0.8, sigma_y = 0.8)
),
burn_in = 50,
num_chains = 2,
seed = 1405,
tune_control = default_tune_control(pilot_m = 200, pilot_burn_in = 10)
)
#> Running chain 1...
#> Running pilot chain for tuning...
#> Using 50 particles for PMMH:
#> Running Particle MCMC chain with tuned settings...
#> Running chain 2...
#> Running pilot chain for tuning...
#> Using 50 particles for PMMH:
#> Running Particle MCMC chain with tuned settings...
#> PMMH Results Summary:
#> Parameter Mean SD Median 2.5% 97.5% ESS Rhat
#> phi 0.80 0.10 0.82 0.60 0.97 10 1.228
#> sigma_x 0.58 0.50 0.46 0.00 1.71 2 1.376
#> sigma_y 0.97 0.35 1.05 0.13 1.46 5 1.272
#> Warning in pmmh(y = y, m = 500, init_fn = init_fn, transition_fn =
#> transition_fn, : Some ESS values are below 400, indicating poor mixing.
#> Consider running the chains for more iterations.
#> Warning in pmmh(y = y, m = 500, init_fn = init_fn, transition_fn = transition_fn, :
#> Some Rhat values are above 1.01, indicating that the chains have not converged.
#> Consider running the chains for more iterations and/or increase burn_in.We get convergence warnings as expected due to the small number of iterations.